Modelos não lineares

Modelos não lineares

Modelos não lineares (NLM) geralmente são voltados a obter algumas informações sobre a relação entre as variáveis Y e X. Tais informações estão vinculadas a diferentes graus de conhecimento como

• uma análise de um gráfico de dispersão de Y vs. X
• restrições de forma da função (monótona, sigmóide)
• a solução de uma equação diferencial suportada por algum princípio ou teoria
• a interpretação dos seus parâmetros.

Qualquer que seja o grau de conhecimento, a escolha de um modelo não linear raramente é empírica.

Um número crescente de pesquisadores compartilha a sensação de que as relações entre variáveis biológicas são melhor descritas por funções não lineares. Processos como crescimento, decadência, nascimento, mortalidade, competição e produção raramente são relacionados linearmente a variáveis explicativas.

Nesse sentido, pode-se dizer que o NLM descrevem melhor processos mecanicistas e são úteis para acomodar restrições relativas a tais processos. Em resumo, os NLM’Ls têm as seguintes vantagens sobre modelos lineares (ML)

• sua escolha é apoiada por princípios teóricos ou mecanicistas (físicos, químicos ou biológicos) ou qualquer outra informação prévia
• certos parâmetros são de interesse para o pesquisador desde que com interpretação
• as previsões podem ser feitas fora do domínio observado de x
• são parcimoniosos, pois normalmente têm menos parâmetros.

Por outro lado, as desvantagens são:

• exigir procedimentos de estimativa iterativa com base no fornecimento de valores iniciais para os parâmetros
• Os métodos de inferência são aproximados
• Exigir conhecimento do pesquisador sobre o fenômeno alvo.

Interpretação de parâmetros

Ao assumir o NLM para descrever um processo, é essencial conhecer o significado de seus parâmetros. Além da dimensionalidade, o estudo do espaço paramétrico é igualmente importante, pois permite reconhecer os valores que um parâmetro assume. Muitos processos envolvem variáveis positivas, como tempo, dose, produção, velocidade e variáveis limitadas, normalmente representadas em porcentagem, como conteúdo (%), concentração (%) e rendimento (%).

Propriedades relevantes de uma função são consideradas, como ter pontos característicos (crítico, inflexão), seu comportamento (concavidade, monoticidade) ou padrões específicos (sigmóide, parabólico).

Algumas dessas propriedades, começando pelos pontos característicos relacionados ao eixo coordenado (Y), são conhecidas como

• ASS: assíntota superior
• ASI: assíntota inferior
• PO: ponto de origem ou interceptação.

Entre os pontos característicos no eixo das abcissas (X) estão:

• PC: ponto crítico
• PI: ponto de inflexão
• PS: ponto de simetria

O símbolo para cada um desses parâmetros dependerá do modelo considerado. Às vezes é mais fácil reconhecer as propriedades de uma função por sua aparência com algum padrão específico. Entre os mais comuns está

• SIG: sigmóide, sendo monótono crescente (MC) ou decrescente (MD). A curva tem uma forma de S ou S invertido. Cada sigmóide tem PI, ASS e ASI.

Paper referência

• Esse paper trata de ajustes de modelos não lineares em dados de COVID-19
• Países com 20 maiores Produto Interno Bruto (PIB)
• Modelagem logística na primeira onda
• Paper

Código R

Para carregar os pacotes necessários nas IDE’s R ou rstudio, basta executar as seguintes linhas de comando.

library(covid19br)
library(tidyverse)
library(dplyr)

data <- downloadCovid19("world") %>%
  filter(country == "Italy")%>%
  select(date, country, accumCases, accumDeaths)
glimpse(data)

## Rows: 799
## Columns: 4
## $ date        <date> 2020-01-22, 2020-01-23, 2020-01-24, 2020-01-25, 2020-01-2~
## $ country     <chr> "Italy", "Italy", "Italy", "Italy", "Italy", "Italy", "Ita~
## $ accumCases  <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3~
## $ accumDeaths <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0~

Comportamento das mortes acumuladas (Itália)

ggplot(data)+
  geom_point(aes(x = as.Date(date), y = accumDeaths), colour = "steelblue")+
  labs(x = "Date (day)", y = "Accumulated deaths")+
  theme_classic()

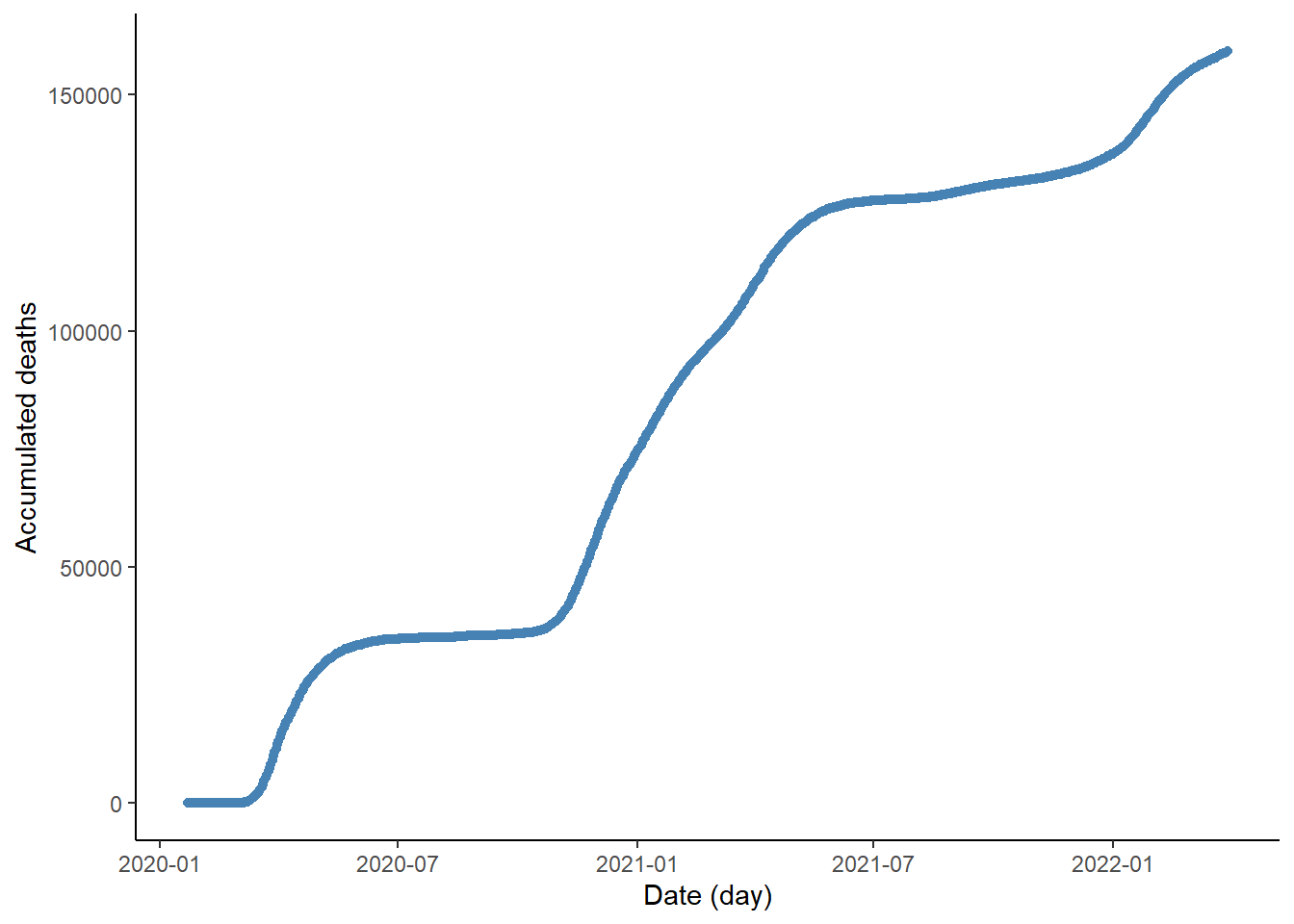
Sugere modelo duplo sigmóide

ggplot(data)+
  geom_point(aes(x = as.Date(date), y = accumDeaths), colour = "steelblue")+
  geom_vline(aes(x = as.Date(date), y = accumDeaths, xintercept = as.Date("2020-10-20")),
             colour="brown", linetype = "longdash")+
  geom_vline(aes(x = as.Date(date), y = accumDeaths, xintercept = as.Date("2021-12-15")),
             colour="brown", linetype = "longdash")+
 annotate("text", label = "sigmoid behavior", x = as.Date("2020-05-1"), y = 100000, size = 5,
          colour = "gray")+
 annotate("text", label = "sigmoid behavior", x = as.Date("2021-08-1"), y = 100000, size = 5, 
          colour = "gray")+
  labs(x = "Date (day)", y = "Accumulated deaths")+
  theme_classic()

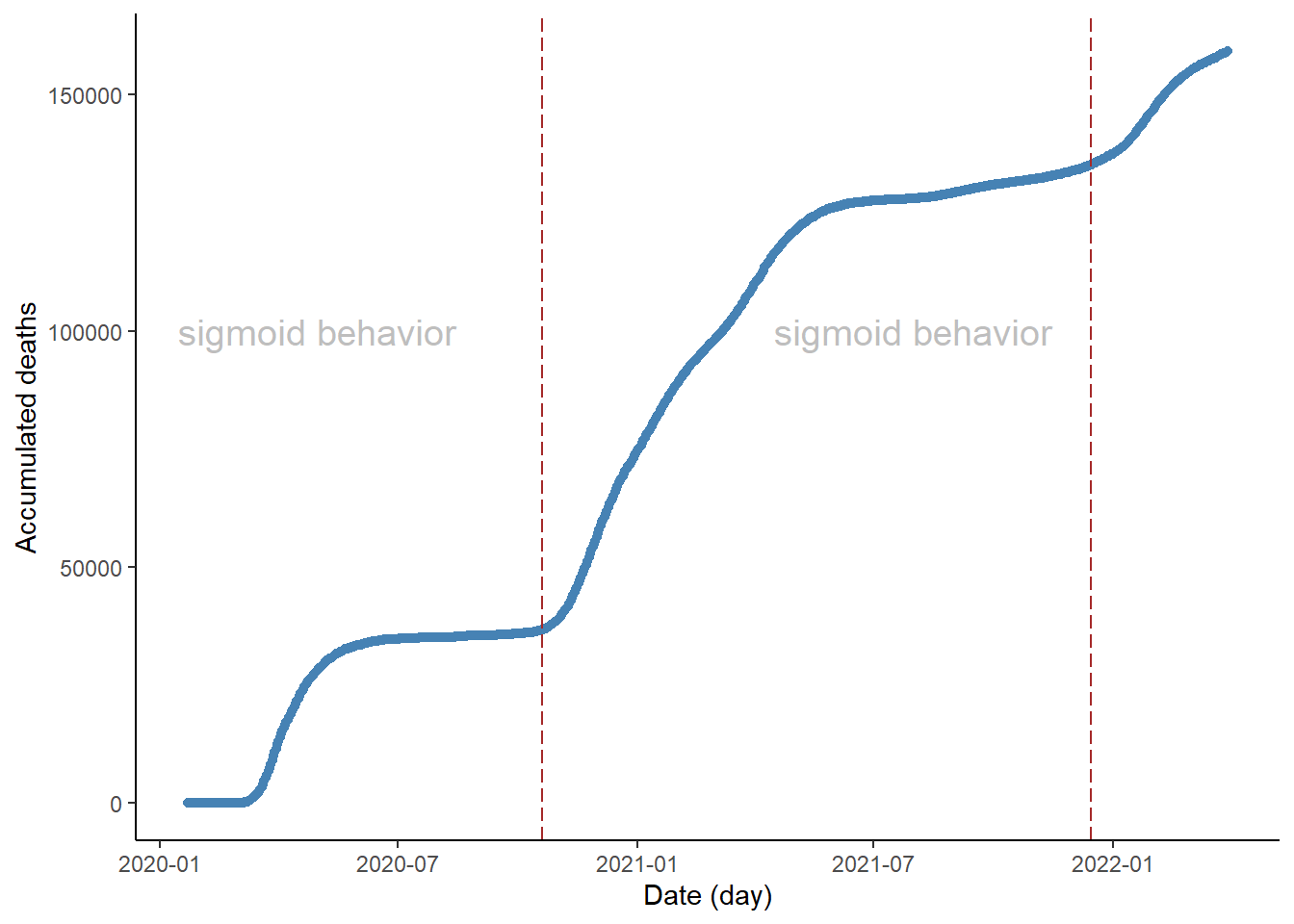
Ajuste do modelo duplo sigmóide

• Criando uma variável numérica para contar o tempo

n <- nrow(data)
data <- data %>%
  mutate(data = c(seq(1,n,1)))
glimpse(data)

## Rows: 799
## Columns: 5
## $ date        <date> 2020-01-22, 2020-01-23, 2020-01-24, 2020-01-25, 2020-01-2~
## $ country     <chr> "Italy", "Italy", "Italy", "Italy", "Italy", "Italy", "Ita~
## $ accumCases  <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3~
## $ accumDeaths <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0~
## $ data        <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,~

• Alterando a escala de dados para evitar problemas de over/under-flow.

data_mod <- data %>%
  select(accumDeaths, data) %>%
  mutate(accumDeathscorr = accumDeaths/10000,
         data = data/100)
glimpse(data_mod)

## Rows: 799
## Columns: 3
## $ accumDeaths     <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ~
## $ data            <dbl> 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, ~
## $ accumDeathscorr <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ~

• Comportamento dos dados transformados

ggplot(data_mod)+
  geom_point(aes(x = data, y = accumDeathscorr), colour = "steelblue")+
  geom_vline(aes(x = data, y = accumDeathscorr, xintercept = 3),
             colour="brown", linetype = "longdash")+
  geom_vline(aes(x = data, y = accumDeathscorr, xintercept = 7),
             colour="brown", linetype = "longdash")+
 annotate("text", label = "sigmoid behavior", x = 1.5, y = 10, size = 5,
          colour = "gray")+
 annotate("text", label = "sigmoid behavior", x = 5.5, y = 10, size = 5, 
          colour = "gray")+
  labs(x = "Day", y = "Accumulated deaths corrected")+
  theme_classic()

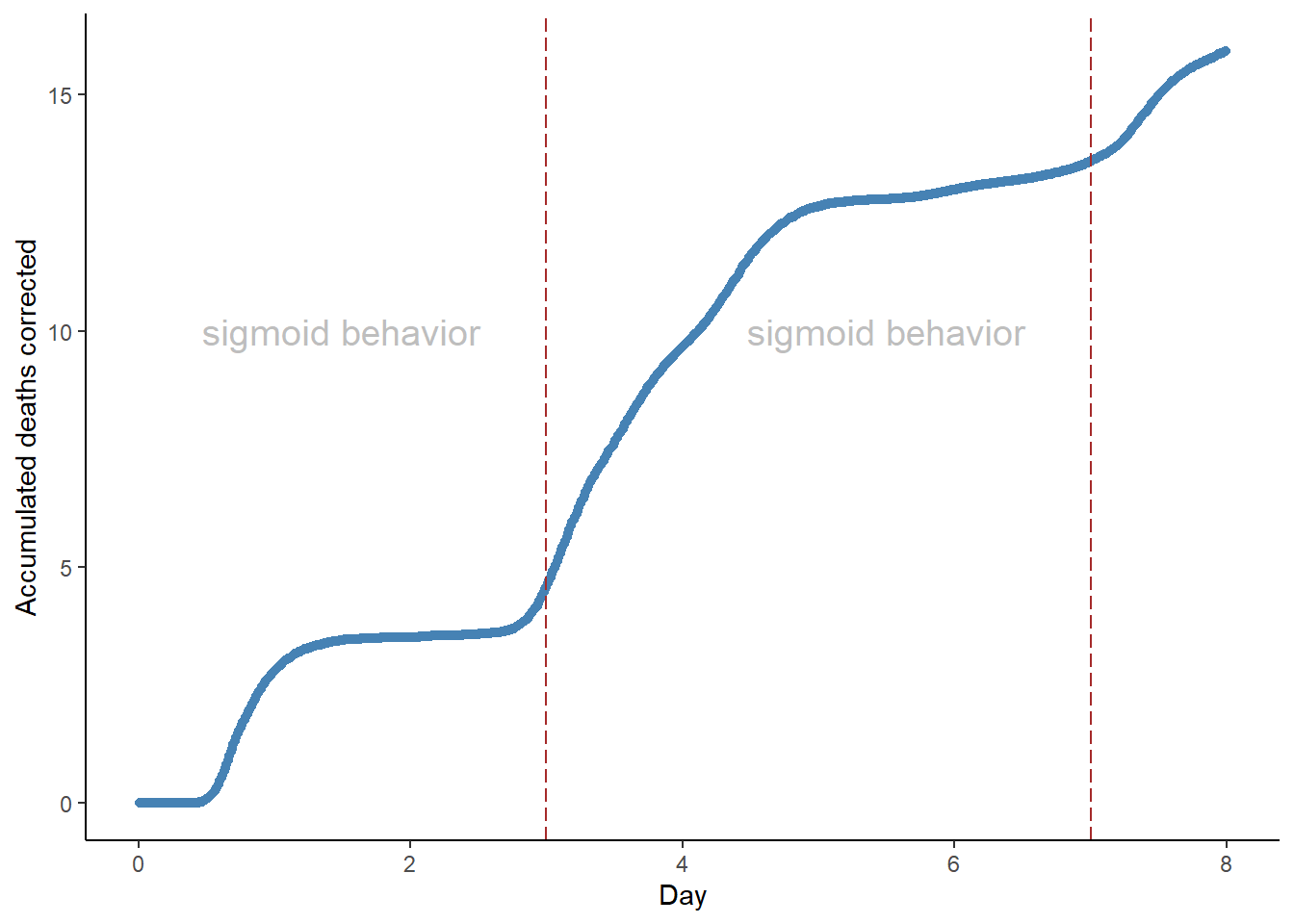
Chutes iniciais para cada sigmóide

• modelo um: modelo logístico

apropos("^SS")

##  [1] "SSasymp"     "SSasympOff"  "SSasympOrig" "SSbiexp"     "SSD"        
##  [6] "SSfol"       "SSfpl"       "SSgompertz"  "SSlogis"     "SSmicmen"   
## [11] "SSweibull"

n0 <- nls(accumDeathscorr ~ SSlogis(data, A, M, S), data = data_mod, 
          subset = data < 3)
coef(n0)

##         A         M         S 
## 3.5857409 0.8126909 0.1364505

data_modn0 <- data_mod %>%
  filter(data < 3) %>%
  mutate(predict = predict(n0))
ggplot(data_modn0)+
geom_point(aes(x = data, y = accumDeathscorr, color = "blue"))+
  geom_line(aes(x = data, y = predict, color = "red"))+
  labs(x = "data", y = "Accumulated deaths")+
  theme_bw()+
  theme(legend.position="right", 
        legend.box = "horizontal",legend.title=element_text(size=15), 
        legend.text=element_text(size=15), axis.text=element_text(size=20),
        axis.title=element_text(size=20), axis.line = element_line(colour = "black"),
        panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        panel.border = element_blank(),
        panel.background = element_blank()) +
  scale_color_manual(values=c("blue", "red"), 
                       name="Accumulated deaths",
                     breaks = c("blue", "red"),
                       labels=c("Observed", "Predict"))

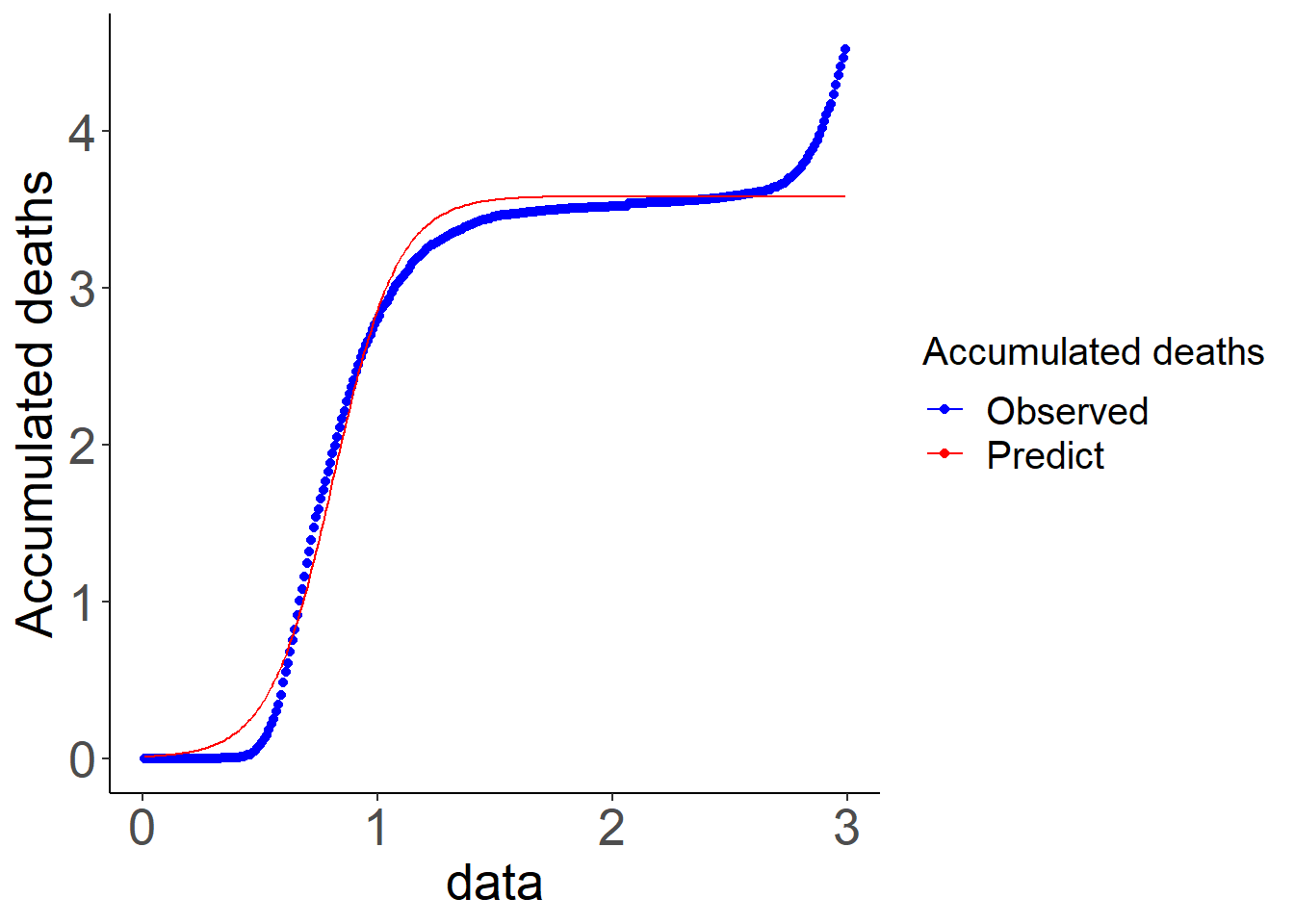
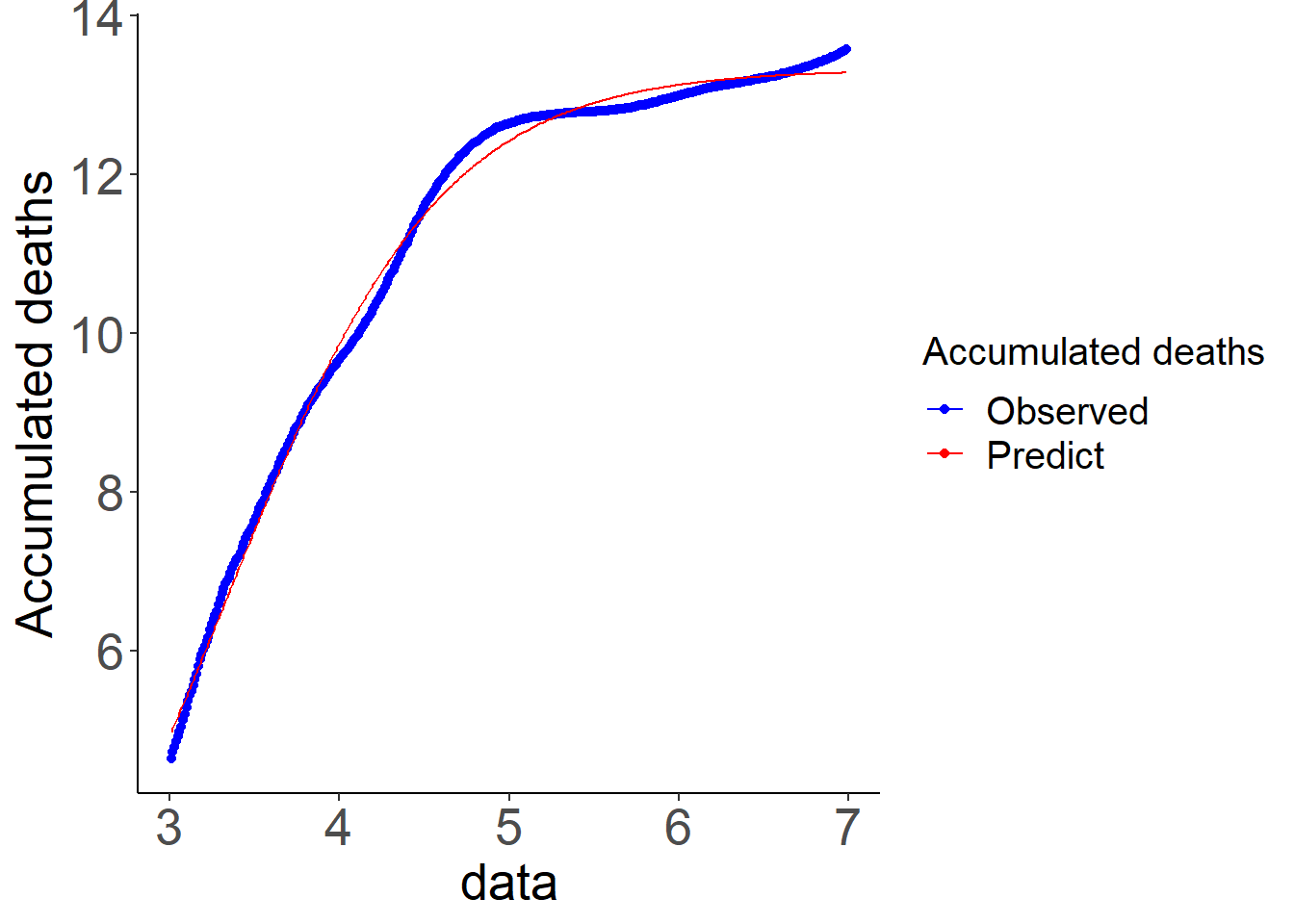
• modelo dois: modelo logístico

apropos("^SS")

##  [1] "SSasymp"     "SSasympOff"  "SSasympOrig" "SSbiexp"     "SSD"        
##  [6] "SSfol"       "SSfpl"       "SSgompertz"  "SSlogis"     "SSmicmen"   
## [11] "SSweibull"

n1 <- nls(accumDeathscorr ~ SSlogis(data, A, M, S), data = data_mod, 
          subset = data > 3 & data < 7)
coef(n1)

##          A          M          S 
## 13.3237430  3.3364864  0.6323343

data_modn1 <- data_mod %>%
  filter(data > 3 & data < 7) %>%
  mutate(predict = predict(n1))
ggplot(data_modn1)+
geom_point(aes(x = data, y = accumDeathscorr, color = "blue"))+
  geom_line(aes(x = data, y = predict, color = "red"))+
  labs(x = "data", y = "Accumulated deaths")+
  theme_bw()+
  theme(legend.position="right", 
        legend.box = "horizontal",legend.title=element_text(size=15), 
        legend.text=element_text(size=15), axis.text=element_text(size=20),
        axis.title=element_text(size=20), axis.line = element_line(colour = "black"),
        panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        panel.border = element_blank(),
        panel.background = element_blank()) +
  scale_color_manual(values=c("blue", "red"), 
                       name="Accumulated deaths",
                     breaks = c("blue", "red"),
                       labels=c("Observed", "Predict"))

Objetivos

• encontre modelos que possam se ajustar a esses dados
• buscar parcerias
• Publicação